



Next: Time and spectral averaging
Up: Data flow and processing
Previous: Calibration
Contents
If the path-length modulation does not match the wavelength of
the channel, a correction must be applied to the fringe
quadratures. For a stroke length in radians of s, where
s = 2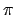 is a matched stroke, the dewarped values are given
by
is a matched stroke, the dewarped values are given
by
| Xc |
= |
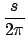 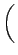 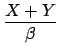 + + 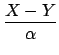 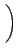 |
|
| Yc |
= |
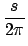 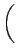 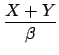 - - 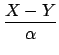  |
|
| Nc |
= |
N - 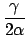 (Y - X) (Y - X) |
|
| NUMc |
= |
NUM - 2GkNc - 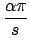 k(Yc - Xc), k(Yc - Xc), |
(11) |
where X, Y, N are the measured quantities and the constants are given by
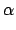 |
= |
2 sin(s/4) - sin(s/2) |
|
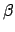 |
= |
1 - cos(s/2) |
|
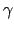 |
= |
2 sin(s/2) |
|
| G |
= |
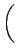 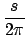 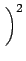 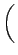 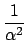 + + 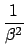  . . |
(12) |
The second term in equation 11 for NUM takes the place
of the kN term in equation 9.
This dewarping correction is applied to all data (fringe tracking and
calibration) before the bias corrections discussed in Sec. 2.4
are applied. This results in a unbiased estimate of the visibility.
Whether or not the dewarping correction is applied is controlled
by the doDewarp parameter (Sec. 3.1).




Next: Time and spectral averaging
Up: Data flow and processing
Previous: Calibration
Contents
RACHEL L AKESON
2004-11-29
![]() is a matched stroke, the dewarped values are given
by
is a matched stroke, the dewarped values are given
by